The Classic Massive Data Problem
Table of Contents
- Introduction
- five approaches to solving the massive data problem
- Classic Scenario Examples
- Summary
1. Introduction
In recent years, high concurrency, distributed, and big data have become a topic that back-end developers can’t get around. When the recruitment software says that high concurrency, big data, and other project experience is preferred, I’m sure a lot of people are secretly shocked, ** projects are CRUD, and there is no chance to get in touch with these scenarios. **.
However, a great man once said: there are no conditions, to create conditions. Since the work can not be exposed to high concurrency and big data, we can bend the road to overtake the car - usually more attention to similar scenarios in the learning time.
This article describes the common means of solving big data problems, as well as some classic big data scenarios and solutions, which **includes bytes, Ali, Baidu and other major domestic Internet companies interviews with the original questions **. After reading this, I believe that we will be able to be familiar with these big data related problems next time we encounter them on a project or in an interview.
2. Five approaches to solving massive data problems
2.1 Partitioning
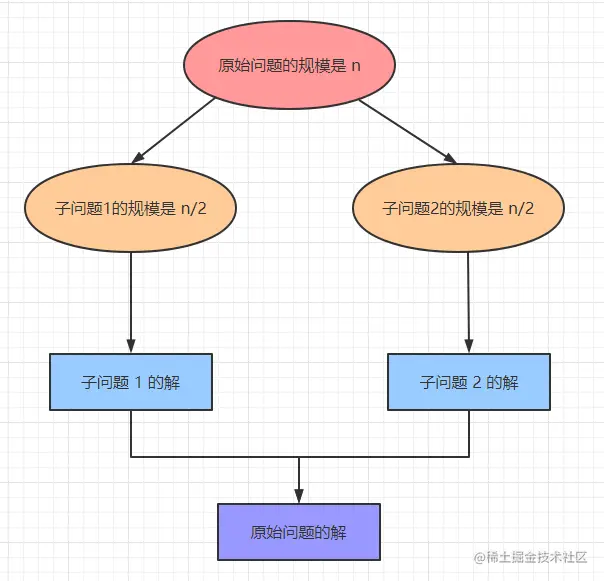
It is well known that ** the computational time required for any computer-solvable problem is related to its size. ** The smaller the size of the problem, the easier it is to solve and the less computation time is required. So, for large-scale data problems, we can also divide and conquer and then just merge the results.
Partitioning algorithm is an efficient tool for solving complex problems, it can decompose a problem into several sub-problems, solve these sub-problems one by one, and then combine them together to form an answer to the big problem.
Computer problems dealing with large amounts of data, the idea of partitioning is basically able to solve, but in general will not be the optimal solution, but can be used as a baseline. for example, in some scenarios we may need to gradually optimize the sub-problems to achieve an optimal solution. The traditional subsumption sort is the idea of partitioning, involving a large number of files that can not be loaded into memory, sorting and other problems can be solved using this method.
Classical scenarios of the partition algorithm: large amounts of data can not be loaded into memory, in order to save time and overhead parallel synchronization to solve the problem and so on.
2.2 Hash (Hash)
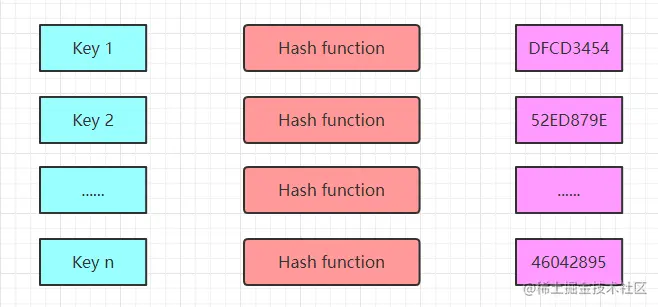
Hash, hash function, as defined by Wikipedia hash is a method of creating a “fingerprint” of small numbers from any data. In layman’s terms, the hash algorithm allows data elements to be located and queried more quickly.
Hash has a time complexity of O(1) for obtaining a key. Assuming that there are n numbers stored in memory by the hash function, we can obtain the value of a key in a constant amount of time.
With such efficient access to data, hash is clearly a great tool for solving big data problems.
And using hash to solve the data access problem is a pretty brutal way to do it: just put it in and take it out! The only downside to **hash is that it’s memory intensive, and you need to load all the data into memory. **Hash
Hash Scenario: Fast lookups, but need enough memory to hold all the data. In this case, if the amount of data is so large that the memory is not enough to store all the data, it can be combined with partition + hash to deal with it. In fact, we often use this approach when solving real-world problems.
2.3 Bitmap (BitMap)
The core idea of the BitMap algorithm is to use a list composed of bits (bit) bits to record the two states 0-1, and then map the specific data to the specific location of this bit array, bit position 0 means that the data does not exist, set to 1 means that the data exists.
** bitmap through the array to indicate the existence of certain elements, it can be used for fast lookup, reweighting and sorting ** and so on. Bitmap is more widely used in big data scenarios, because it can save a lot of space utilization.
The next two classic scenarios, weighing and sorting to see the effectiveness of bitMap in which it plays a role.
Scenario 1: Finding non-repeating positive integers among 200 million integers
**Bitmap Weighting
Since there is not enough memory to hold these integers, we can use bitmaps. Using a 2-BitMap (each number is assigned 2 bits, 00 for nonexistent, 01 for occurring once, 10 for occurring multiple times), iterate through all the elements, set the position of the element that has been iterated over to 01, and if it is iterated over again set it to 10. Finally, count all the elements that have 01 (occurring only once) in their position.
Scenario 2: Sorting some integer elements [6,4,2,1,5
Bitmap Sorting
Since the elements of the array to be sorted are all less than 8 (and may be much more than that in real scenarios), we can request an 8bit array (one byte) and then iterate over these elements, setting the position subscripts of the existent elements to 1 [0 1 1 1 1 0 1 1 1 0].
After traversing, we again traverse this bit array, you can get the final sorting results:
1 | for i := 0; i i++ { |
2.4 Bloom Filter
Bloom filter was proposed by Bloom in 1970, it is actually composed of a very long binary vector and a series of random hash functions.
Bloom filter is mainly used to determine whether the target data exists in a massive dataset and set of intersection. To determine the existence of an example: Bloom filter through the target data mapping, can be O(k) time complexity to determine the existence of the target data, where k for the use of the number of hash functions, which can greatly reduce the traversal of the time required to find.
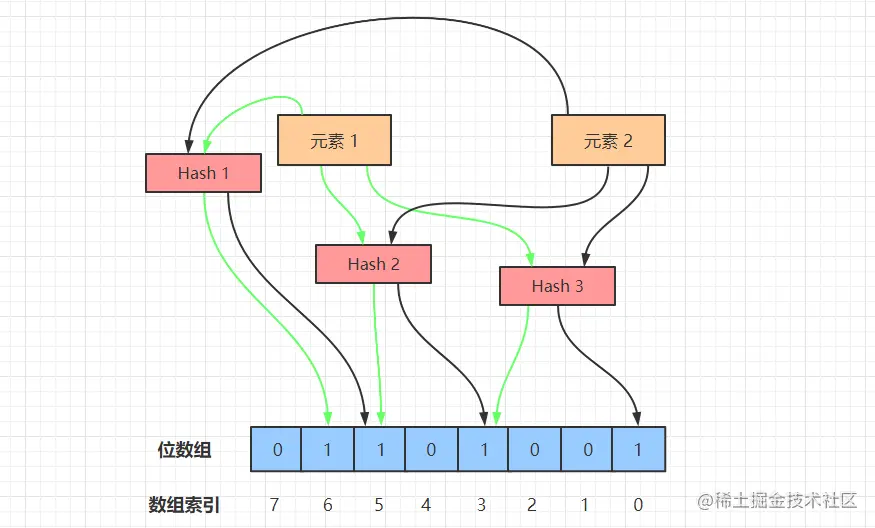
The workflow of the Bloom filter is shown in the figure above, we next simulate the Bloom filter to do element adding and querying operations.
- Adding elements
Bloom filter to add elements, the use of different hash functions on the element value of the hash calculation, so as to get more than one hash value.
For example, in the figure above, the element 1, after three hashes, after a series of operations to calculate the remainder of the three numbers 3, 5, 6. Then, we will be in the array of 3, 5, 6 three subscripts set to 1, the addition of the element 1 operation is complete. - Searching for elements
In the use of Bloom filters to query the existence of an element, first of all, the given element to perform a number of hash operations, and get the same as when the element is added to the position of the bit array.
For example, for element 1 to perform three Hash operations, the position of the bit array were 3, 5, 6, to determine whether the value of these positions are all 1, if one of them is 0, the element does not exist; if they are all 1, the probability that the element exists. - Element misjudgment
When the Bloom Filter adds elements, the array position of the element after the Hash may be set to 1 by other elements, for example, after the element x has been Hashed 3 times, the hit position array subscripts are 0, 3, 6, and the values of these three subscripts are set to 1 when inserting the element 1 and element 2.
Therefore, when querying element x, it will be misjudged that element x already exists, which is the root cause of the misjudgment - multiple hash values of an element may be hit by other elements accidentally, so it is not possible to determine that the element must exist.
Although BloomFilter has a certain rate of misjudgment, but the probability is very small, about 0.01% ~ 0.05% between, so in some big data scenarios, the use of BloomFilter can significantly improve the efficiency of the judgment, provided that you can accept a small margin of misjudgment.
2.5 Heap
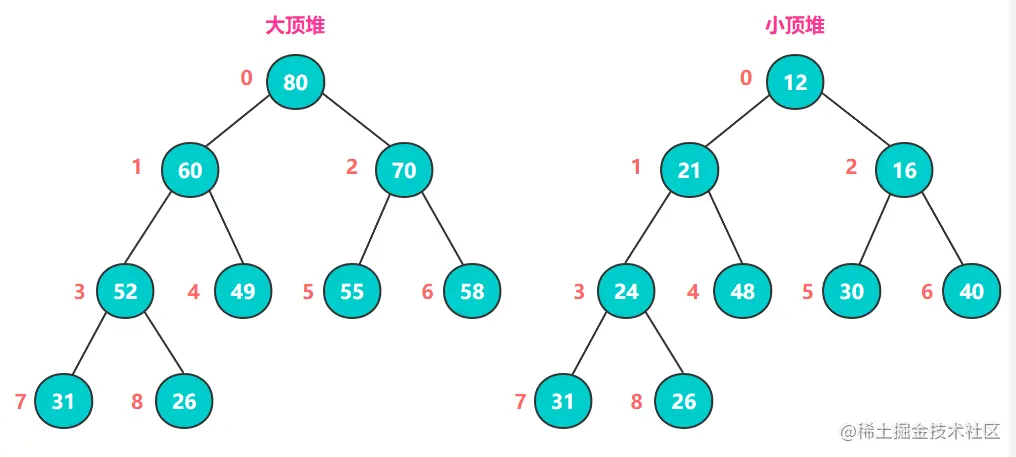
Heap is a kind of complete binary tree with two structures: big top heap and small top heap. A big top heap is characterized by its parent nodes being greater than or equal to the values of its left and right child nodes, while a small top heap is the opposite, with its parent nodes being less than or equal to the values of its left and right child nodes.
When building a big top heap or small top heap, we need to use heap sort.
The core idea of heap sort (big top heap example) is: keep comparing the values of all the parent nodes and child nodes, and exchange the larger number into the parent node, after completing one round of comparison, the maximum value of the whole sequence is the root node at the top of the heap.
Then, swap the root node with the end node (the node labeled 8 in the graph), which is then the maximum value.
Then, the remaining n-1 elements are reconstructed into a big top heap, so that the maximum value of the n-1 elements is obtained, and the cycle is repeated to obtain an ascending sequence.
Q: Why don’t we use small top heap for ascending?
A: Because there is no way to guarantee the incrementality of each level. For example, the 5th and 8th elements of the small top heap in the above figure are 26 elements.
In large amount of data, heap sort is a commonly used solution to the TopN problem, and it can satisfy most of the problems of finding the most value.
3. Examples of Classic Scenarios
1) Finding non-repeating integers in a large number of numbers.
Problem Description
Find non-repeating integers out of 10 billion integers. Note that there is not enough memory to hold so many integers.
Question Answer
1. Partitioning + HashMap
10 billion integers, each int integer occupies 4 bytes, 100 x 10^8 x 4B is about 400GB. if we read it into memory as a file, it definitely won’t fit.
So we can split the large file into small files, such as through the Hash operation, will be 10 billion integers assigned to 1000 files, each file to store 10 million integers, these files will be numbered 0 ~ 999, and then they were traversed into the HashMap, where the key is an integer, the value for the number of times it occurs.
Then, the 1000 HashMap were counted out only 1 time in the integer, and then merge the final result.
**Bitmap method
Since integers occupy more memory, we can use one or more bits to mark whether an element occurs and the number of times it occurs, which can greatly save storage space.
We use 2 bits to indicate the state of occurrence of a number: 00 means it has not appeared, 01 means it has appeared once, and 10 means it has appeared many times. 10 billion integers are of int type, each integer occupies 4 bytes, i.e., 32 bits, and the memory required is 2^32 x 2bit = 1GB.
When the available memory is greater than 1GB, the bitmap method can be used to solve this problem. By iterating through the 10 billion numbers, the corresponding subscripts 00->01 (integer occurs once), 01->10 (integer occurs many times), and finally counting the number of 01 (occurs only once).
**Bloom filter
Iterate through the 10 billion integers, they will be deposited into the Bloom filter, before depositing through a number of Hash to determine whether the value of the bit array exists, if it exists that the probability of the existence of the integer; if the value of a Hash does not exist in the bit array, that the integer must not exist.
2) Duplicate URLs found in two large files
Problem Description
Given two files a.txt, b.txt, each holding 5 billion URLs, with each URL occupying 64B, and a memory limit of 4G, find the URLs common to files a and b. Find the URLs that are common to both files.
Answer
The file size of 50 x 10^8 x 64B is about 320GB, so 4G memory is not enough to load all URLs into memory at once.
Partitioning + HashMap
This question is very similar to the previous one, except that the integers are replaced by URLs, and we handle it in a similar way.
First, divide the file where the URLs are stored into multiple small files, so that each small file is no larger than 4G, so that the two small files corresponding to a and b can be processed in memory, and the results can be merged in the end.
First traverse the file a, traversed to the URL by hash mode: hash (URL) % 100, according to the results of the calculation of the URL into a0, a1 … a99.txt, each of which is about 3.2 GB in size. b is traversed in the same way, and the URL is split into b0, b1 … b99.txt. b99.txt.
After splitting, all possible identical URLs are in the corresponding small files, i.e., a0 corresponds to b0, …, and a99 corresponds to b99. All we need to do is to find the URLs that are the same in these 100 pairs of small files.
To find the same URL, we can use HashSet/HashMap, when the URL exists in Set/Map, it means the URL is duplicated, so we can save the duplicated URLs in a separate file, and then merge all the same URLs in the end.
3) Top100 for frequency of request for large session files
Problem Description
There is a file of 100 million conversations, each line of the file is a conversation, the size of each conversation is not more than 1KB, the memory size is limited to 1.5 GB, and it is required to return the 100 conversations with the highest frequency (Top100).
Question Answer
Due to memory constraints, it is not possible to read large files into memory at once. Therefore, the same partitioning strategy is used to split large files into smaller ones for processing.
1. Partitioning + HashMap
First, we use the same way as the previous question to partition the file for processing.
1.5 GB/1 KB is about 1.5 million sentences, and the memory of each file cannot exceed 1.5 million conversations, so we hash each sentence with hash(sentence) % 100, and store the result into a[i] (0<=i<=99) files, each file stores about 1 million conversations.
Then use HashMap to count the 100 most frequent conversations in each file, key is the md5 value of the conversation, value is the frequency of occurrence. The final result is 100*100 = 10,000 conversations, and then the 10,000 words are heap sorted to find out the Top100 frequency conversations.
2. Small Top Heap
Construct a small top heap of size 100, the top element of the heap is the minimum frequency value of the conversation, if in the process of traversing the HashMap, found that the value of the current conversation (the number of times the conversation occurs) is greater than the number of times the top of the heap conversation occurs, then replace the old conversation with a new conversation, and then re-adjust the small top heap.
At the end of the traversal, the 100 words on the small top heap are the 100 conversations with the highest frequency of occurrence of the session we need to count.
4).Extract the highest frequency IP from massive log data
Problem Description
This is an original question from an interview with Baidu, the question is that there is a massive log data containing access IPs saved in a huge file, which can’t be read into the memory, and it is required to extract the IP with the highest number of accesses to Baidu on a certain day.
Question Answer
Partitioning + HashMap
We first use the partition strategy to split the file storing IP data into multiple small files, and then traverse all the small files to extract all the IPs that visited Baidu on that day into a single file.
Then use HashMap to count the number of times each IP accesses, through a variable maxCount to store the value of the highest number of accesses, and constantly compared to find the IP with the highest number of accesses.
5) Count the number of different numbers in a large number of phone numbers
Problem Description
Count the number of phone numbers in a file that contains about 10 billion phone numbers, note that the phone numbers may be duplicates.
Problem Solution
Bitmap method
Since the length of a phone number is 11 digits, and there are 10 cases of numbers on each digit, we need to apply a bit array of length 100 billion (10^11), which requires about 12.5GB of memory 10^11 x 1bit. traverse all the numbers, set the array to 1 when the number occurs, and record the bitmap element that is set to 1 for the first time with a count, and the final result will be obtained at the end of the traversal. After the traversal is finished, the final result will be obtained.
4. Summary
Massive data problems, basically by the above kinds of classical problems morphing, common solution, is the partition, Hash, BitMap, Bloom filter and heap sort. Other types of big data problems may be a combination of various means of solution in different ways.
More complex may be based on text deformation, such as the search engine prefix tree structure, big data text retrieval inverted index and so on, due to space limitations, this paper is not listed.
However, for the classic problems mentioned above, these several solutions are already enough. If you encounter similar interview questions or problem scenarios, we can be handy:)